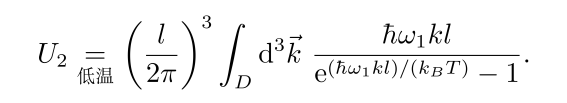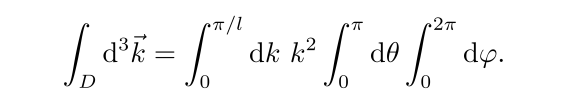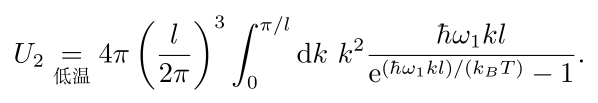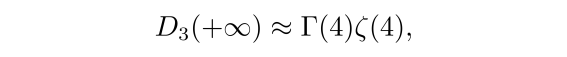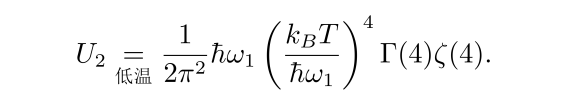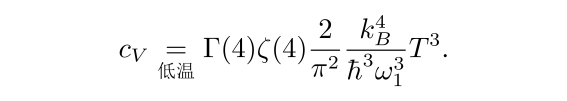baccarat online australia

在自然界中，原本处于力学平衡的物理对象，受微扰后在平衡点附近发生的运动都可以被简单的谐振子模型近似。其中，最经典也最成功的案例是由爱因斯坦提出、经由德拜发扬光大，并启发了现代凝聚态物理学的固体晶格振荡模型。前面一系列直播课上，张朝阳曾详细讲解了一维谐振子链的量子化方法，并利用代数解法给出了对应的能谱。他解释道，利用傅里叶变换以及按模式定义的升降算符 a(k) 和 a^+(k)，可以在“ k 空间”中将一维谐振子链的哈密顿量改写为

而按模式定义的“微分哈密顿量”

其中 l 为链上两点间间距，

为按模式定义的粒子数算符，而能隙满足色散关系

事实上，这样一条谐振子链即可以看为是一个一维晶体。但为了建模现实中真实存在的、具有三维结构的晶体，还是希望把谐振子链模型扩展为谐振子晶格模型。此时，可以想象，晶格（如图）即是空间被分割成一些列等边长 l 的立方体，原子（或者分子）被放置在立方体的各顶点上，受到三个方向上近邻格点上原子（或者分子）的作用，该作用同样以谐振子势刻画。

此时，需要用三个整数 (q1, q2, q3) 来标记晶格上的每个顶点，对应地，引入傅里叶变换时，需要将波数取为三维矢量

此时，总的哈密顿量即可以看作

这里因子 3 源于粒子在三个方向上都由振动，而 h(k) 仍取与谐振子链相同的形式，但值得注意地是，这里不带下标的 k 应当理解为矢量的模长。利用矢量符号，三重积分又可以简写为

积分区域 D 即以原点为中心，边长为 2π/l 的正方体，习惯上又称为“第一布里渊区”。在下文中，为简洁起见，将沿用这些记号。

历史上，爱因斯坦参考了对黑体吸收辐射光子的量子化处理，首次天才般地将晶体中的分子运动以谐振子模型刻画。爱因斯坦将晶体视为 N 个独立运动的粒子的集合，或者等价地视为是 3N 个独立谐振子的集合。“独立”即相互作用强度 ω1 = 0，于是，而单个谐振子哈密顿量是

而考虑 3N 个谐振子这一大集合，更一般地做法是按统计力学考虑粒子能级排布满足某一热分布。这是因为在写下单粒子哈密顿量时，往往会忽略很多相互作用——比如体系内部的高阶相互作用、或者与外界的相互作用。但在它们依然是真实存在的，考虑多粒子体系时，这些相互作用会将体系维持在热态。对这样一个体系最细致和严格地处理需要用到量子统计力学，用一个密度矩阵

来刻画它的动力学行为。幸运的是，在当前关注的问题中，可以暂且地绕开这一复杂的计算和物理图像，转而拥抱适用但更简单的半经典处理。所谓半经典处理，即考虑粒子的分布按能级能量满足经典的玻尔兹曼分布

其中 N0 为分布在基态上的粒子数。于是，单粒子的平均能量

这里计算过程与早期课程中所讲解的，求黑体辐射平均能量的计算是一致的，在这里不再赘述。

于是，整个体系的能量

当温度很高即

时，其中第二项还可以近似为与温度的线性关系

为了验证模型的有效性，爱因斯坦考虑将其应用到固体比热容的计算上，以和具体的实验结果作对比。固体比热（Specific heat）刻画的是固体改变单位质量温度时放出或吸收的能量，对固体，一般考虑定容比热容

将前面的计算结果代入到这一定义，不难看出，在高温极限下有

这一结果即和经典热力学中的能量均分原理达成一致。这是由于在温度很高时，粒子更倾向于受更大能量的热扰动激发。这一个激发能量将远大于谐振子能谱的能隙，使得能谱可以被近似地看为是连续的。

另一方面，在低温极限

下，系统能量可以被近似为

此时，计算比热容有

即当温度趋于 0 K 时，固体的比热容会按指数极快的趋近于 0，提供了热力学第三定律的一种解释。

此时，如果将上面的分析与具体的实验结果相对比，用黑线大致描绘爱因斯坦模型给出的热容随温度分布于下图，而用红线描绘实验测量的结果。

不难发现爱因斯坦模型在高温极限下与观测有符合地相当好，在低温极限的区域则不然。在爱因斯坦的模型中，在低温时，粒子大量集中在基态上。由于基态到第一激发态间有能隙 ℏω，粒子需要接受一个能级相当可观的扰动才能“爬上”这一悬崖峭壁。而在低温极限下，出现这种微扰的概率是被大幅压低的，也即晶体很难与外界交换能量。这说明，爱因斯坦对固体晶体的建模是一个非常粗略的近似：他专注于描绘单个原子的动力学，而忽略了系统的集体行为。诚然，这足够达成他的目的，以表达出他对量子化的思考。

（张朝阳利用爱因斯坦模型计算固体比热）

固体比热的德拜模型

对固体比热更精细的分析，要归功于德拜对爱因斯坦模型的思考和改进。如果说爱因斯坦模型是在对格点上每个谐振子分别作对角化求其本征态，德拜模型则是更细致地在理论中加入了谐振子之间的领头阶相互作用，然后在这个基础上求解谐振子的能谱。同时，如果考虑晶体是由单原子（Monoatomic）组成，事实上每个原子间仅受相邻原子的作用，爱因斯坦模型中所谓的独立谐振子，不过是从中截取出一个片段时看到的假象。于是，在德拜模型中应取 ω = 0，而

其中 k_{BO} 是利用Born-Oppenheimer近似计算的原子间劲度系数， m 是原子的质量。对应的色散关系取为

注意在此处，按照此前约定，矢量模长 k > 0，故取平方根时无需再考虑负数部分。

在前面的课程中，张朝阳已经充分解释过这样一个图像：从晶格的整体运动行为可以视为是由波数（矢量）k 标记的、一系列独立简正模式的加和。按色散关系，这些简正模式有高低不等的能量。其中高能部分几乎不传播，可以认为是被局限在某点上的剧烈振荡，低能部分可以与固体中经典机械波对应——此即固体中的波粒二象性。回到对比热的讨论，爱因斯坦模型的问题即在于忽略了固体中低能部分简正模式的贡献。换句话说，一块晶体从外界吸收能量后，并不一定只能激发单个粒子在平衡点附近剧烈振动。

相反，从整个晶体的角度，谐振子集体微小振动所组成的格波，也是系统允许存在的量子态。此时，可以看到，后者的能隙极小甚至是连续的，于是在低温极限下也会允许存在相对一部分激发态。“形象地说，按爱因斯坦模型，在低温极限下本来以为只能“攀上去”的悬崖峭壁，走进一看原来还修有一系列便于我们行走的阶梯。”张朝阳称。

按照这个思路，可以尝试从晶体集体行为的角度重新推导固体的比热。“首先，在谐振子模型中，每一个简正模式都独立接受能量独立被激发。”张朝阳介绍，“于是，将统计力学应用到晶体上时，每一个由特定 k 标记的简正模式将会由于被我们所忽略的相互作用，经一定弛豫时间后达到热平衡——这一过程与爱因斯坦模型中对单个谐振子的讨论是一致的。”而不同的简正模式之间，由于它们的激发相互独立，所以可以视为不存在直接的热力学关联，计算整个系统的配分函数或者内能时，只需要将它们简单地加和，即

第二行中，可以直接利用了爱因斯坦模型中对单个谐振子平均能量的计算结果，只是将能量部分作了相应的改写。

注意到在积分中，第一项与温度无关，可以仅考虑化简第二项，并代入色散关系，有

“直接计算这样一个积分非常困难，所以我们转而研究一些特殊情况下它的行为。”张朝阳介绍，比如在高温极限下，考虑一个很大的温度（T → ∞），有

对其作积分，有

于是高温极限下的比热容

与爱因斯坦模型的结果保持一致，同样回到了能量均分定律。

另一方面，可以考虑低温极限（T → 0）。此时，观察 U2 中的积分函数，在温度很低时

也即整个积分函数

被极大地压低。“此时，事实上仅当我们同时让波数模长 k → 0，其与温度之比才有可能得到一个有限值，使得函数对积分有贡献。这样一个结论和我们前面的讨论保持一致：在低温极限下，只有低能部分的集体激发是重要的，它们是粒子能够走上的阶梯。而高能部分的激发耸立在悬崖上，几乎触不可及。”张朝阳称。

按照这个思路，首先 k → 0 时化简色散关系为

于是，积分可以改写为

为了计算简便，可以在积分中转而采用极坐标形式，即

张朝阳提醒，事实上用极坐标或者说球体来近似原本是立方体的布里渊区，原则上会遇到描述积分边界的困难。幸运的是，因为在低温极限下，布里渊区的边界对内能的贡献被指数压低，所以对边界是否有正确的描述并不关键。事实上，对模长积分的上限的取值或者说积分区域的球体半径，也不一定要取为布里渊的变成，它应当是系统的一个自由参数，这一点会在后续的课程中展开讨论。

利用极坐标，可以将积分改写为

利用换元

可以将其进一步化简为

其中积分上标

而整个积分可以被定义为德拜函数

当温度很低时，有 x → +∞，且注意到数学上德拜函数

其中 Γ 为欧拉gamma函数，ζ 为黎曼zeta函数。

于是，低温极限下的计算结果可以表达为

对温度求导后得到比热容

不难看出其正比于温度的三次方，

与实验上所观察到的趋势吻合得相当好。

此即固体比热的德拜模型，它可以视为爱因斯坦模型的细化，解决了爱因斯坦模型在低温极限下的缺陷。在中间区域，由于积分很复杂，并没有一个解析的结果。

（张朝阳利用德拜模型计算固体比热）

据了解，《张朝阳的物理课》于每周周五、周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。

online crypto casino online betting site best football betting site

---

声明：该文观点仅代表作者本人，搜狐号系信息发布平台，搜狐仅提供信息存储空间服务。